Forecasting Percentages

Recipe: use likelihood=β€˜beta’ for (0,1) targets

This how‑to shows how to use the Beta likelihood for a proportion / percentage target using the same sktime-style API demonstrated in other tutorials.

Why Beta? Because the target is naturally bounded in (0,1), and Beta likelihood can provide probabilistic intervals in (0,1). The likelihood="beta" option internally applies a link that guarantees valid predictions.

1. Load data and build a (0,1) target

import numpy as np
import pandas as pd
from sktime.split import temporal_train_test_split

num_obs = 1000
y = pd.DataFrame(
    data={"value" : np.sin(np.arange(num_obs)*2*np.pi/30)*0.45 + 0.5},
    index=pd.period_range(
        "2025-01-01",
        periods=num_obs,
        freq="D",
    )
) 
y += np.random.normal(0, 0.1, size=y.shape)
y = y.clip(1e-6, 1 - 1e-6)

y_train, y_test = temporal_train_test_split(y, test_size=0.4)

y_train.plot.line()

2. Specify model components

We use a piecewise linear trend plus weekly and yearly seasonality. The API mirrors the univariate tutorial: pass trend=..., supply exogenous_effects as a list of tuples, and choose likelihood="beta".

import numpyro
from prophetverse.effects.trend import PiecewiseLinearTrend
from prophetverse.effects.fourier import LinearFourierSeasonality
from prophetverse.effects.target.univariate import BetaTargetLikelihood
from prophetverse.utils import no_input_columns
from prophetverse.engine import MAPInferenceEngine
from prophetverse.sktime import Prophetverse


numpyro.enable_x64()

seasonality = (
    "seasonality",
    LinearFourierSeasonality(
        freq="D",
        sp_list=[30],  # weekly + yearly
        fourier_terms_list=[30],
        prior_scale=1,
        effect_mode="additive",
    ),
    no_input_columns,
)

model = Prophetverse(
    trend="flat",
    exogenous_effects=[seasonality],
    likelihood=BetaTargetLikelihood(noise_scale=0.2),  # <β€” key change
    inference_engine=MAPInferenceEngine(),
    scale=1,
)
model.fit(y=y_train)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm
Prophetverse(exogenous_effects=[('seasonality',
                                 LinearFourierSeasonality(fourier_terms_list=[30],
                                                          freq='D',
                                                          prior_scale=1,
                                                          sp_list=[30]),
                                 '^$')],
             inference_engine=MAPInferenceEngine(),
             likelihood=BetaTargetLikelihood(noise_scale=0.2), scale=1,
             trend='flat')
Please rerun this cell to show the HTML repr or trust the notebook.

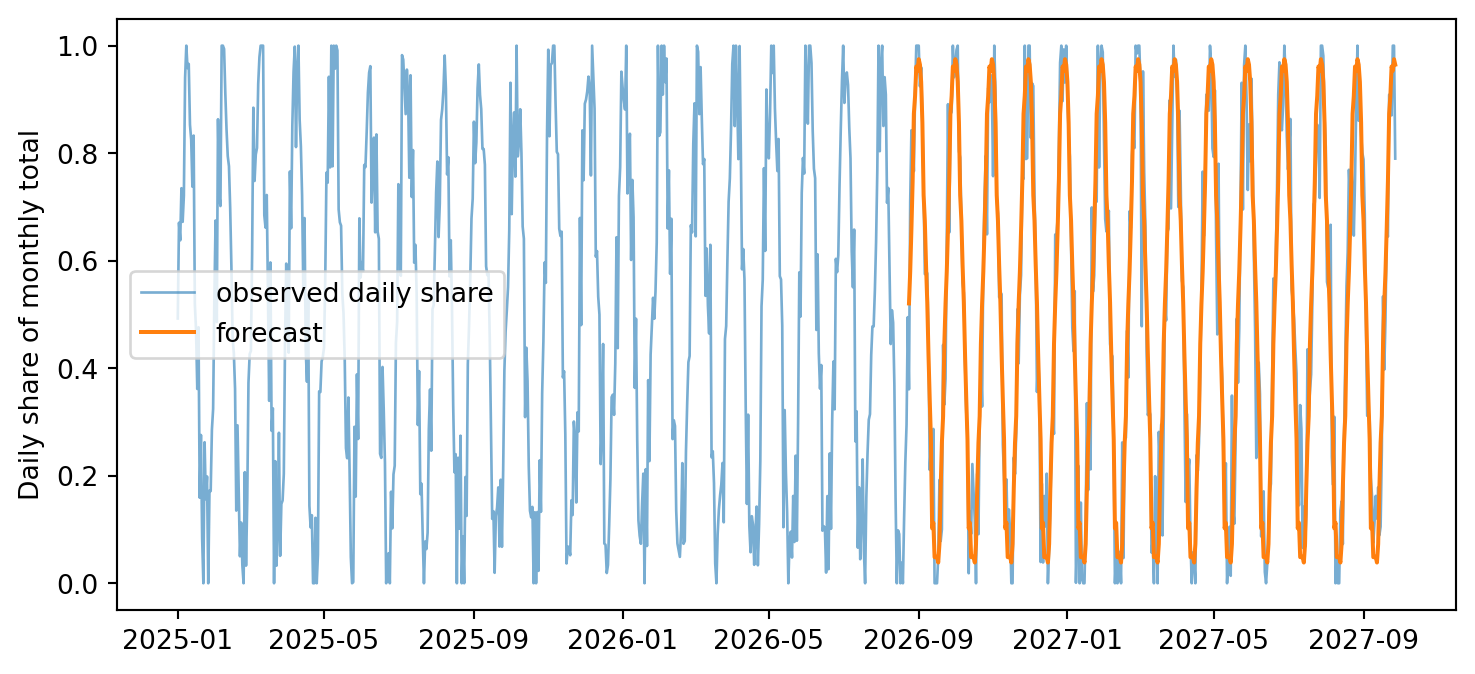
3. Forecast the next 180 days

import pandas as pd

fh = y_test.index
pred_share = model.predict(fh=fh)
pred_share.head()
value
2026-08-24 0.471094
2026-08-25 0.610348
2026-08-26 0.673942
2026-08-27 0.732843
2026-08-28 0.828405

4. Plot

import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(9, 4))
ax.plot(
    y.index.to_timestamp(), y, label="observed daily share", lw=1, alpha=0.6
)
ax.plot(pred_share.index.to_timestamp(), pred_share, label="forecast", color="C1")
ax.set_ylabel("Daily share of monthly total")
ax.legend()
plt.show()

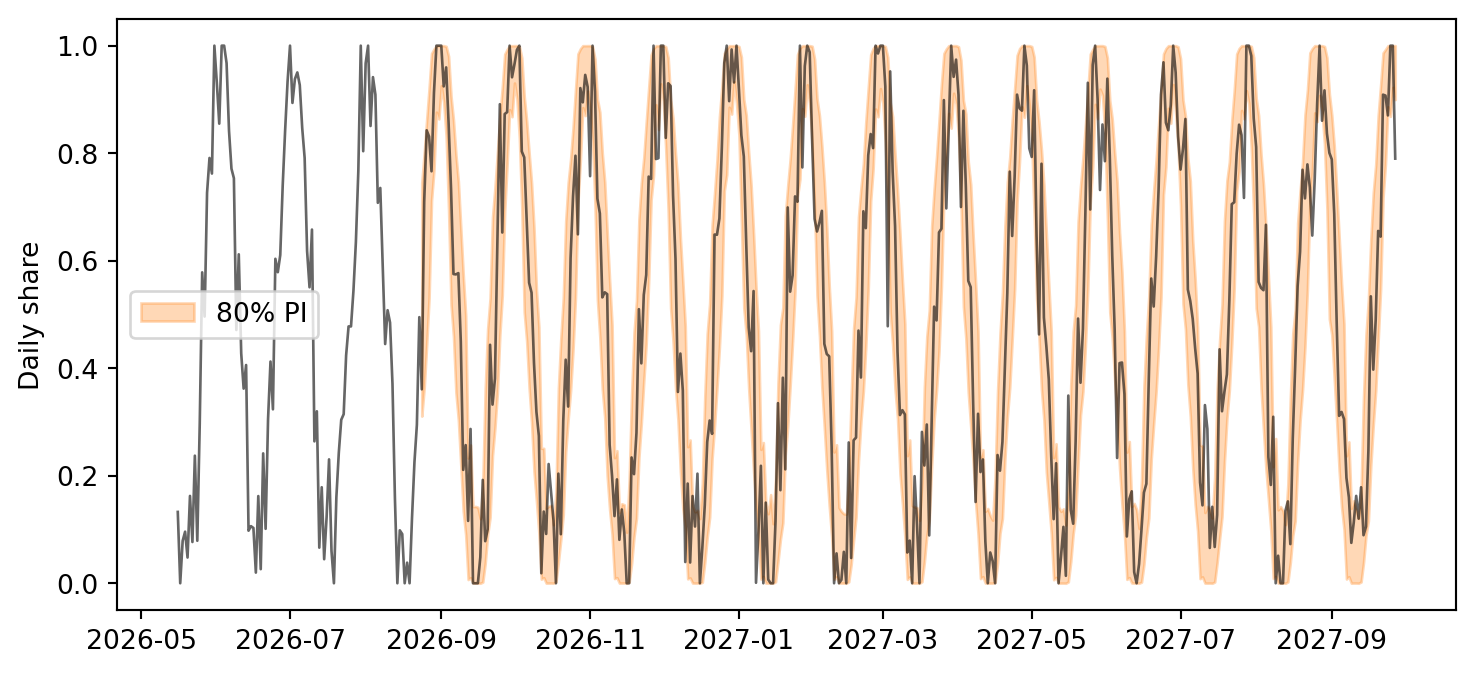
5. Probabilistic forecast (quantiles)

q = model.predict_quantiles(fh=fh, alpha=[0.1, 0.9])
fig, ax = plt.subplots(figsize=(9, 4))
ax.fill_between(
    q.index.to_timestamp(),
    q.iloc[:, 0],
    q.iloc[:, -1],
    color="C1",
    alpha=0.3,
    label="80% PI",
)
ax.plot(y.iloc[-(len(fh) + 100):].index.to_timestamp(), y.iloc[-(len(fh) + 100):], lw=1, alpha=0.6, color="k")
ax.set_ylabel("Daily share")
ax.legend()
plt.show()

Notes & Tips

  • Ensure the target is strictly inside (0,1), excluding the boundaries.
  • noise_scale controls dispersion of the Beta (smaller => tighter intervals).
  • The same pattern works for conversion rates, CTR, retention proportions, etc.
  • Switch to full Bayesian inference by setting inference_engine=MCMCInferenceEngine(...) if you need richer uncertainty.